| 2 초 | 128 MB | 17725 | 9162 | 6838 | 52.242% |
문제
각각 부피가 A, B, C(1≤A, B, C≤200) 리터인 세 개의 물통이 있다. 처음에는 앞의 두 물통은 비어 있고, 세 번째 물통은 가득(C 리터) 차 있다. 이제 어떤 물통에 들어있는 물을 다른 물통으로 쏟아 부을 수 있는데, 이때에는 한 물통이 비거나, 다른 한 물통이 가득 찰 때까지 물을 부을 수 있다. 이 과정에서 손실되는 물은 없다고 가정한다.
이와 같은 과정을 거치다보면 세 번째 물통(용량이 C인)에 담겨있는 물의 양이 변할 수도 있다. 첫 번째 물통(용량이 A인)이 비어 있을 때, 세 번째 물통(용량이 C인)에 담겨있을 수 있는 물의 양을 모두 구해내는 프로그램을 작성하시오.
입력
첫째 줄에 세 정수 A, B, C가 주어진다.
출력
첫째 줄에 공백으로 구분하여 답을 출력한다. 각 용량은 오름차순으로 정렬한다.
예제 입력 1
8 9 10
예제 출력 1
1 2 8 9 10
알고리즘 분류
아이디어
각 물통의 상태 ⇒ 노드
물을 옮기는 것 ⇒ 엣지
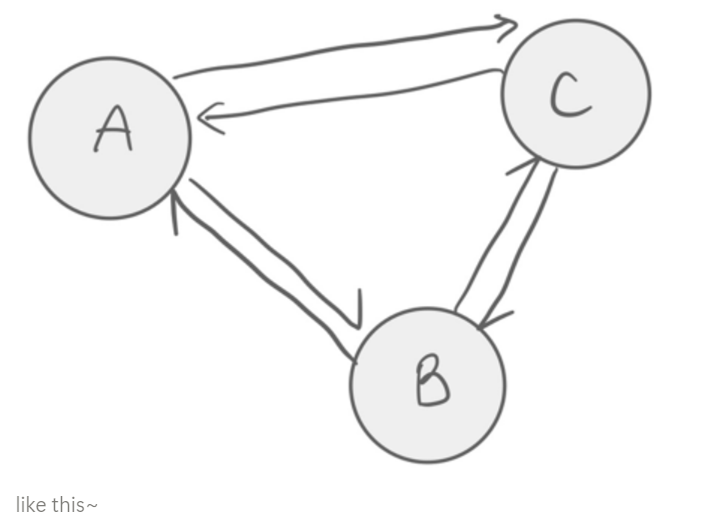
like this~
즉, BFS 알고리즘을 이용해서 구현할 수 있다.
문제 풀이
'''
백준 2251번
골드5 물통
'''
import sys
from collections import deque
input = sys.stdin.readline
def bfs(A, B, C):
visited = set()
caseC = set() # 물통A가 비어있을 때 물통 C의 물의 양을 저장하는 집합
queue = deque([(0, 0, C)])
while queue:
a, b, c = queue.popleft()
# 이미 방문했다면 skip
if (a, b, c) in visited:
continue
visited.add((a, b, c))
# 물통 A가 비어있는 경우
if a == 0:
possible_C.add(c)
# A->B
queue.append((max(0, a + b - B), min(B, a + b), c))
# A->C
queue.append((max(0, a + c - C), b, min(C, a + c)))
# B->A
queue.append((min(A, b + a), max(0, b + a - A), c))
# B->C
queue.append((a, max(0, b + c - C), min(C, b + c)))
# C->A
queue.append((min(A, c + a), b, max(0, c + a - A)))
# C->B
queue.append((a, min(B, c + b), max(0, c + b - B)))
return sorted(caseC)
A, B, C = map(int, input().split())
result = bfs(A, B, C)
print(' '.join(map(str, result)))
물을 옮기는 여섯 가지 경우를 모두 큐에 추가해준다. 이때 min, max를 활용해서 넘치는 물을 고려해준다.
'코딩테스트 > 백준(Python)' 카테고리의 다른 글
| [백준][Python] 상근이의 여행(실버4) (0) | 2024.08.02 |
|---|---|
| [백준][Python] 11052번.카드 구매하기 (실버1) (0) | 2024.07.31 |
| [백준][Python] 12919번. A와 B 2 (골드5) (0) | 2024.07.18 |
| [백준][Python] 1138번. 한 줄로 서기 (실버2) (0) | 2024.07.18 |
| [백준][Python] 17615번. 볼 모으기 (실버1) (0) | 2024.07.18 |
| 2 초 | 128 MB | 17725 | 9162 | 6838 | 52.242% |
문제
각각 부피가 A, B, C(1≤A, B, C≤200) 리터인 세 개의 물통이 있다. 처음에는 앞의 두 물통은 비어 있고, 세 번째 물통은 가득(C 리터) 차 있다. 이제 어떤 물통에 들어있는 물을 다른 물통으로 쏟아 부을 수 있는데, 이때에는 한 물통이 비거나, 다른 한 물통이 가득 찰 때까지 물을 부을 수 있다. 이 과정에서 손실되는 물은 없다고 가정한다.
이와 같은 과정을 거치다보면 세 번째 물통(용량이 C인)에 담겨있는 물의 양이 변할 수도 있다. 첫 번째 물통(용량이 A인)이 비어 있을 때, 세 번째 물통(용량이 C인)에 담겨있을 수 있는 물의 양을 모두 구해내는 프로그램을 작성하시오.
입력
첫째 줄에 세 정수 A, B, C가 주어진다.
출력
첫째 줄에 공백으로 구분하여 답을 출력한다. 각 용량은 오름차순으로 정렬한다.
예제 입력 1
8 9 10
예제 출력 1
1 2 8 9 10
알고리즘 분류
아이디어
각 물통의 상태 ⇒ 노드
물을 옮기는 것 ⇒ 엣지

like this~
즉, BFS 알고리즘을 이용해서 구현할 수 있다.
문제 풀이
'''
백준 2251번
골드5 물통
'''
import sys
from collections import deque
input = sys.stdin.readline
def bfs(A, B, C):
visited = set()
caseC = set() # 물통A가 비어있을 때 물통 C의 물의 양을 저장하는 집합
queue = deque([(0, 0, C)])
while queue:
a, b, c = queue.popleft()
# 이미 방문했다면 skip
if (a, b, c) in visited:
continue
visited.add((a, b, c))
# 물통 A가 비어있는 경우
if a == 0:
possible_C.add(c)
# A->B
queue.append((max(0, a + b - B), min(B, a + b), c))
# A->C
queue.append((max(0, a + c - C), b, min(C, a + c)))
# B->A
queue.append((min(A, b + a), max(0, b + a - A), c))
# B->C
queue.append((a, max(0, b + c - C), min(C, b + c)))
# C->A
queue.append((min(A, c + a), b, max(0, c + a - A)))
# C->B
queue.append((a, min(B, c + b), max(0, c + b - B)))
return sorted(caseC)
A, B, C = map(int, input().split())
result = bfs(A, B, C)
print(' '.join(map(str, result)))
물을 옮기는 여섯 가지 경우를 모두 큐에 추가해준다. 이때 min, max를 활용해서 넘치는 물을 고려해준다.
'코딩테스트 > 백준(Python)' 카테고리의 다른 글
| [백준][Python] 상근이의 여행(실버4) (0) | 2024.08.02 |
|---|---|
| [백준][Python] 11052번.카드 구매하기 (실버1) (0) | 2024.07.31 |
| [백준][Python] 12919번. A와 B 2 (골드5) (0) | 2024.07.18 |
| [백준][Python] 1138번. 한 줄로 서기 (실버2) (0) | 2024.07.18 |
| [백준][Python] 17615번. 볼 모으기 (실버1) (0) | 2024.07.18 |
